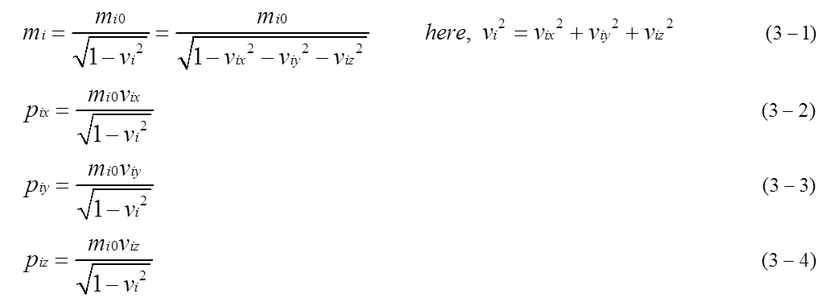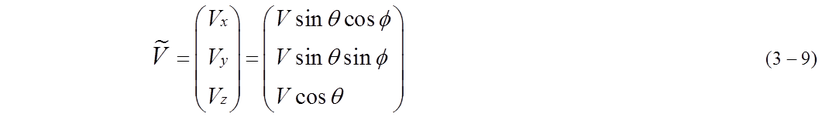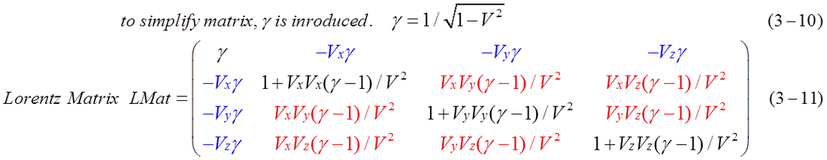3. Extension of the theory to x-y-z three dimensional space
In case of one dimension, mass and momentum are easily expressed by equation (2-12). On the other hand, mass and momentum of particles in three dimensions are expressed by equation (3-1), (3-2), (3-3) and (3-4).
To consider rest mass of a group of mass in three dimensional space, three momentum of a group of mass, (Px,Py,Pz) must be zero, although individual momentum of particles is not zero.
To consider rest mass of a group of mass in three dimensional space, three momentum of a group of mass, (Px,Py,Pz) must be zero, although individual momentum of particles is not zero.
M0 is an equivalent rest mass. M0 and a representative velocity (Vx,Vy,Vz) can be defined as equation (3-5), (3-6), (3-7), (3-8). There are 4 unknown variables decided by these equations. These variables are Vx,Vy,Vz and M0. Equation (2-17) is also satisfied in case of three dimensional space.
There is a little complicated formula that can be used for Lorentz transformation of vector (m,p) in 3 dimensional space.
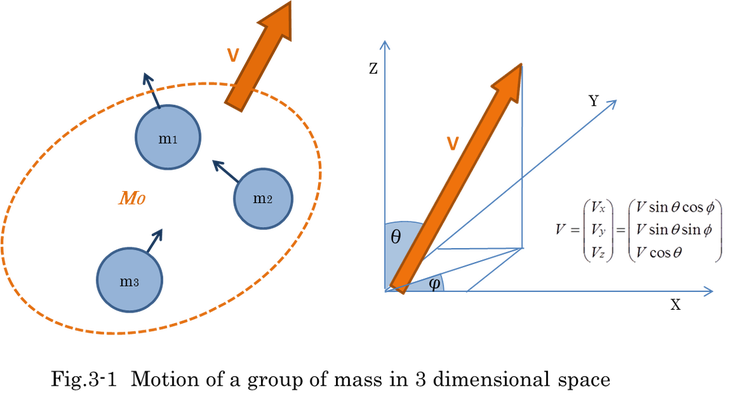
Fig.3-1 shows the motion of a group of mass. V is a representative velocity of a group of mass. Each direction of motion of mass is different. Of course, the direction of V is different from the velocity vi. The direction of V is calculated from equation (3-6), (3-7),(3-8) by substituting equation (3-5). The direction is defined as equation (3-9).
Fig.3-1 shows the motion of a group of mass. V is a representative velocity of a group of mass. Each direction of motion of mass is different. Of course, the direction of V is different from the velocity vi. The direction of V is calculated from equation (3-6), (3-7),(3-8) by substituting equation (3-5). The direction is defined as equation (3-9).
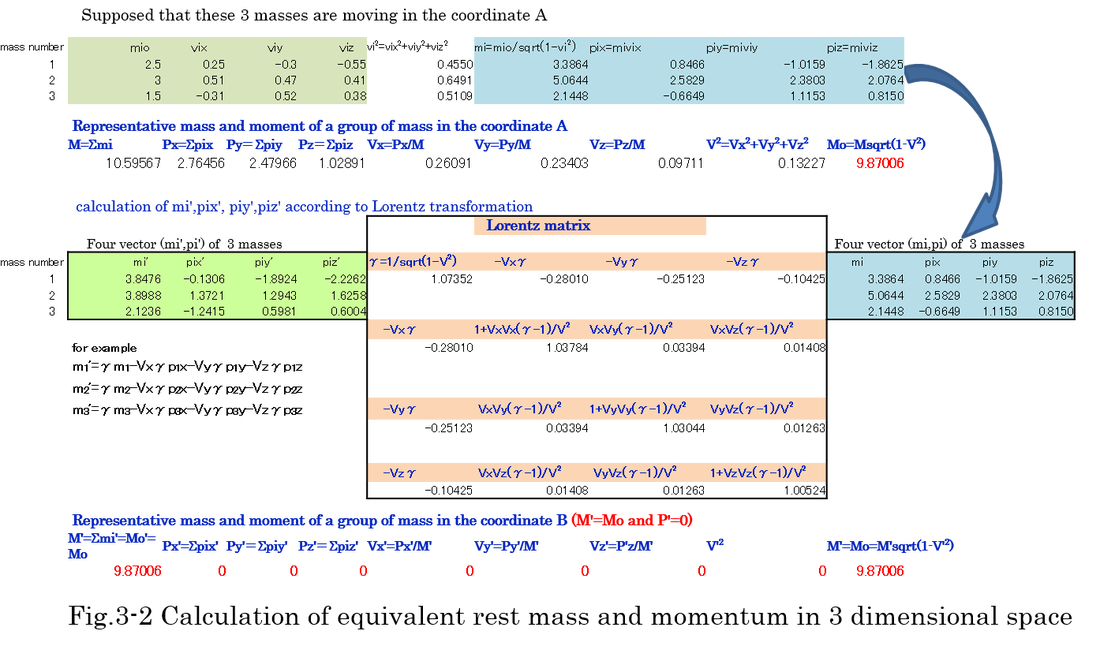
Lorentz transformation matrix (wikipedia.org/wiki/Lorentz_transformation 5) is equation (3-11). Four-vector (mi,pi) in the coordinate A can be transformed to (mi', pi') which is observed from the center of the moment of M0. M0 is equivalent rest mass. After calculation of M0 and V, elements of Lorentz matrix LMat are determined. Then, (mi, pi) can be transformed to (mi', pi') using Lorentz matrix. We can make sure that the four-vector (M', P')=(M0, 0). That is, the summation of mi' surely equals M0 and the summation of pi' equals zero. For an example, three masses are moving in the coordinate A. Calculation table of four-vector (mi, pi), (mi', pi'), (M, P) and (M0, 0) are shown in Fig.3-2.
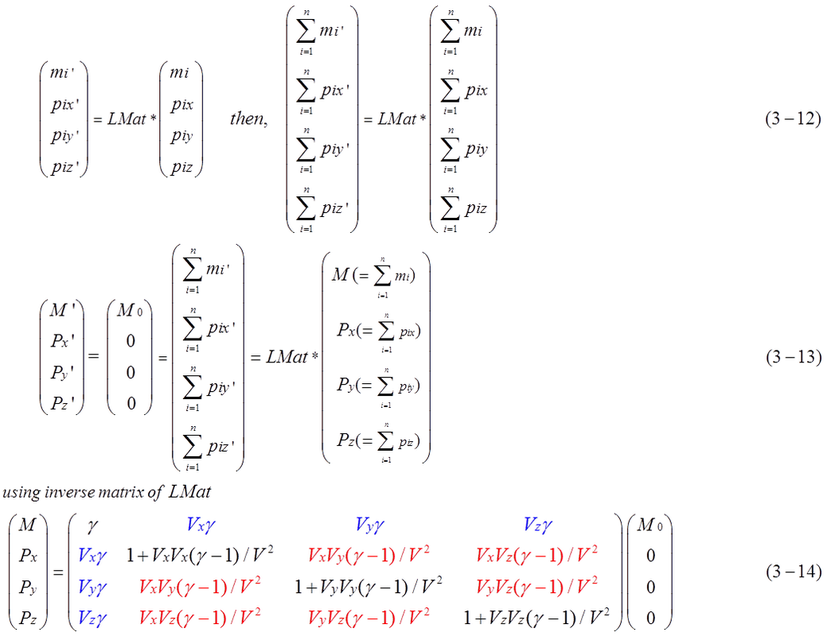
The conclusion of calculation is equation (3-12), (3-13). The inverse matrix is used for inverse transformation from (M0,0) to (M,P) as equation (3-14). Calculation of inverse matrix is easy because all we need to do is change (-Vx,-Vy,-Vz ) to (Vx,Vy,Vz) in equation (3-11).
Anyway, once the representative velocity V and M0 are decided, LMat and inverse matrix of LMat can be commonly used for transformation from (mi, pi) to (mi', pi').
Anyway, once the representative velocity V and M0 are decided, LMat and inverse matrix of LMat can be commonly used for transformation from (mi, pi) to (mi', pi').
If you need to check the calculation of matrix, click the following file.
| lorentz_mat_20130101.xlsx | |
| File Size: | 34 kb |
| File Type: | xlsx |