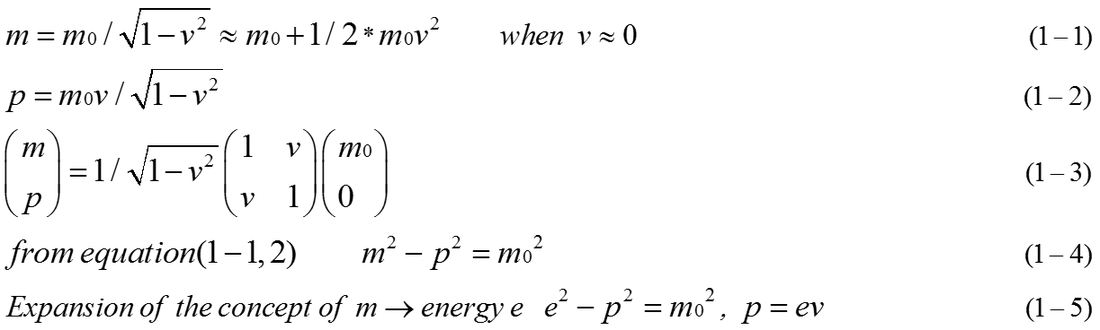1. Preparation for modeling of a group of mass.
At first, a single mass shown in Fig.1-1 is moving with velocity v in a certain inertial coordinates A. Relativistic mass and momentum (m,p) is well known as equation (1-1),(1-2). Including momentum p, m and p are expressed by matrix equation (1-3). (wikipedia.org/wiki/Mass in special relativity4)
m0 is a rest mass and v is the velocity of the center of a rest mass in a coordinates A. v is defined as non-dimensional velocity divided by light speed(c). Equation (1-1) is important to express that m has kinetic energy and rest energy m0.
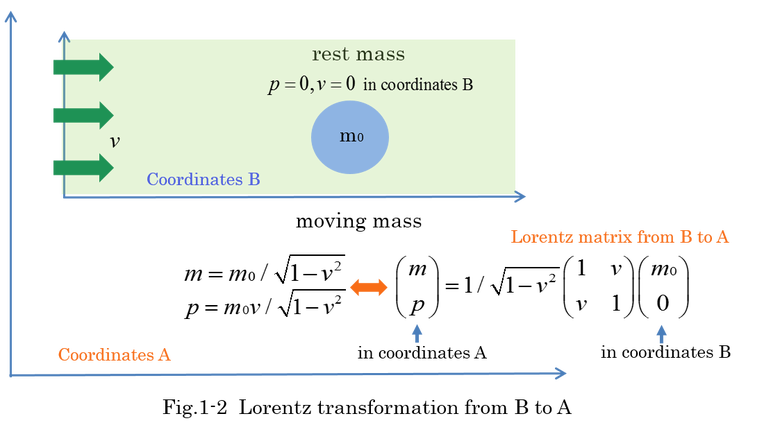
In addition, m0 can be transformed into m according to Lorentz transformation in Equation (1-3). This matrix equation implies that rest mass which is stationary in a moving coordinates can be considered as a moving mass in other coordinates .
Equation (1-4) is not introduced without considering Lorentz transformation of (m,p). In equation (1-5), p is redefined as a flow of energy. Refer to equation (ap17-1) to (ap17-4) in appendix 17 in page 6. We can apply equation (1-5) to photon when m0=0,v=1. However, in this section, relativistic mass(m) is treated as a inertia and momentum(p) is m*v.
Fig.1-2 indicates that rest mass(m0) is moving in coordinates A, but, it is at rest in moving coordinates B.
In addition, m0 can be transformed into m according to Lorentz transformation in Equation (1-3). This matrix equation implies that rest mass which is stationary in a moving coordinates can be considered as a moving mass in other coordinates .
Equation (1-4) is not introduced without considering Lorentz transformation of (m,p). In equation (1-5), p is redefined as a flow of energy. Refer to equation (ap17-1) to (ap17-4) in appendix 17 in page 6. We can apply equation (1-5) to photon when m0=0,v=1. However, in this section, relativistic mass(m) is treated as a inertia and momentum(p) is m*v.
Fig.1-2 indicates that rest mass(m0) is moving in coordinates A, but, it is at rest in moving coordinates B.
Everyone knows that a moving mass has kinetic energy and it turns to be a rest mass when v=0. Some people think it is merely a geometric relation including space-time. However, there remains a basic question about what rest energy is. Does a mass at rest have energy? The explanation for such a question is given in page 3.
When we observe a moving mass m at the same velocity v, m0 is stationary. Even if the center of rest mass is resting, it should be considered that inner part of rest mass is not resting. It is shown in page-3 that rest mass can be decomposed into kinetic energy and smaller rest masses by mathematical procedures. Unless the equation m=m0/sqrt(1-v^2) is deeply considered, we cannot imagene the idea that a rest mass consists of a lot of small moving masses.
When we observe a moving mass m at the same velocity v, m0 is stationary. Even if the center of rest mass is resting, it should be considered that inner part of rest mass is not resting. It is shown in page-3 that rest mass can be decomposed into kinetic energy and smaller rest masses by mathematical procedures. Unless the equation m=m0/sqrt(1-v^2) is deeply considered, we cannot imagene the idea that a rest mass consists of a lot of small moving masses.