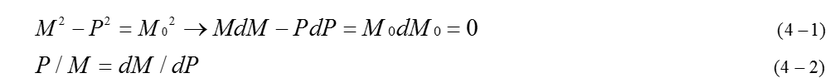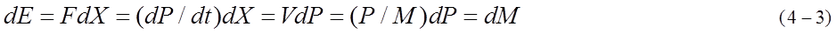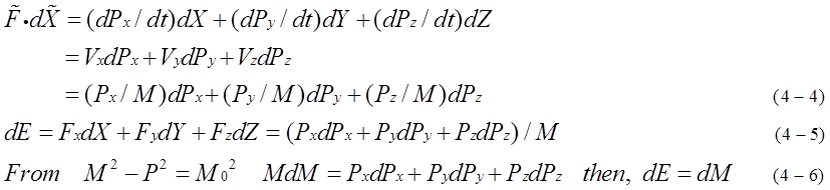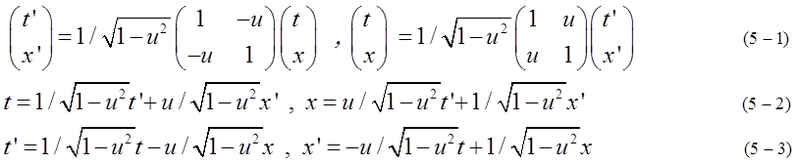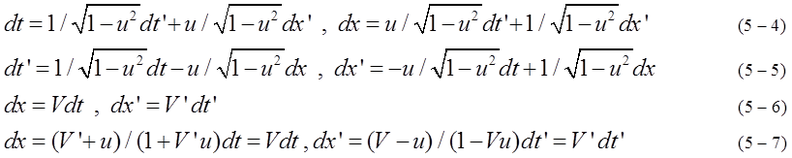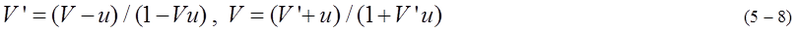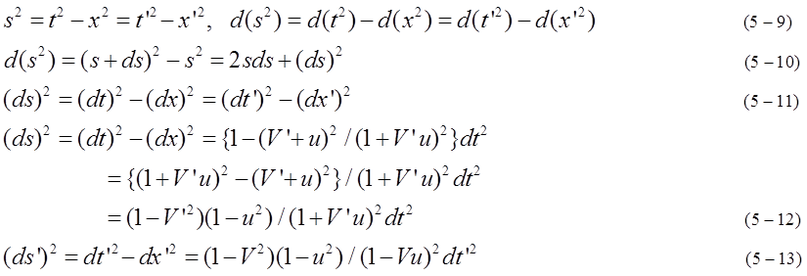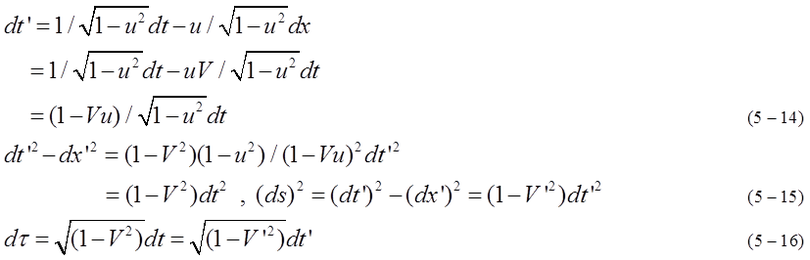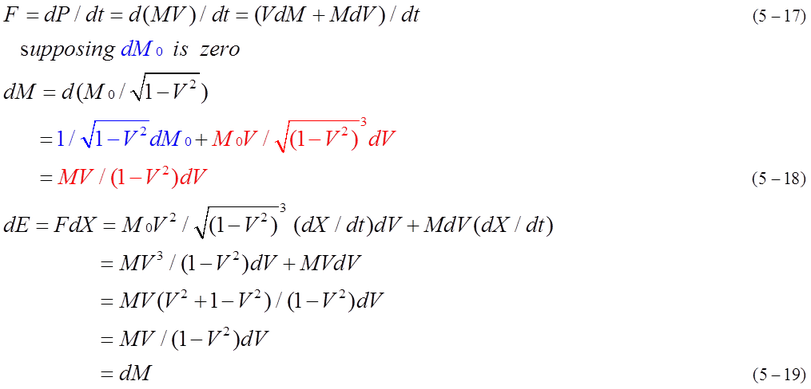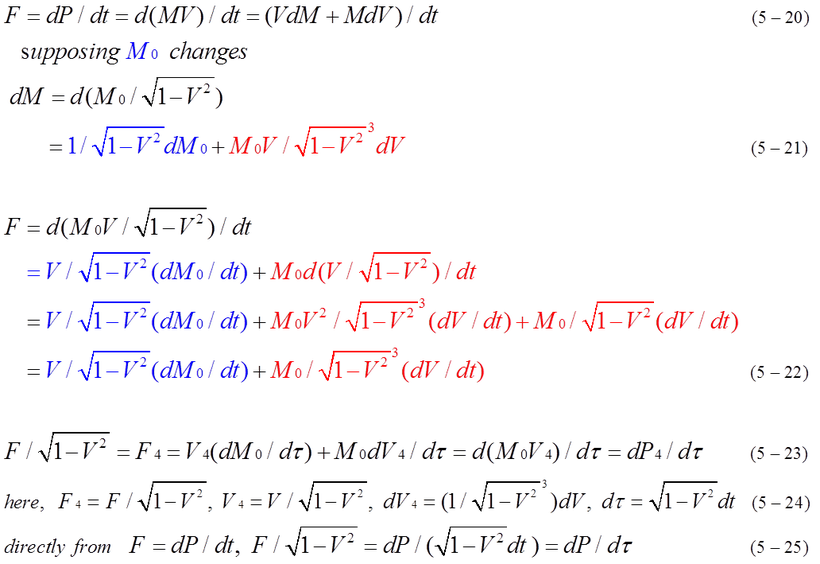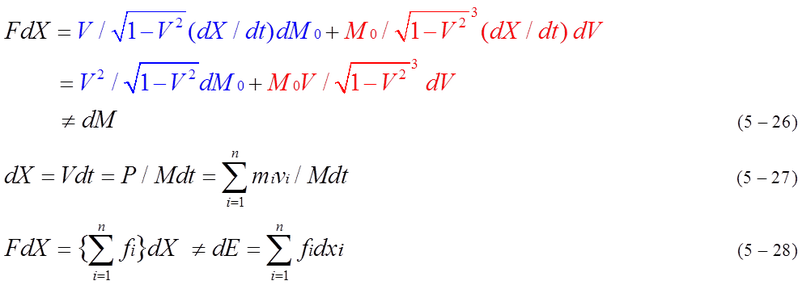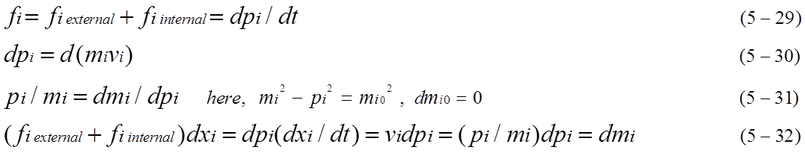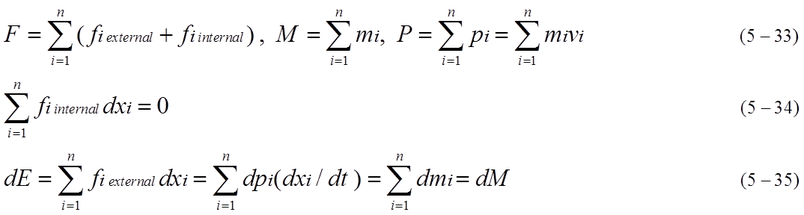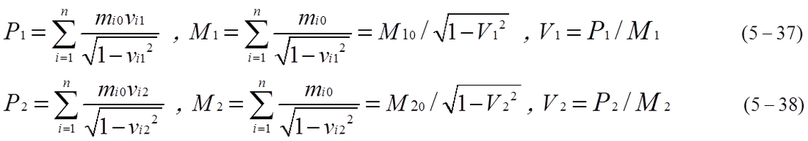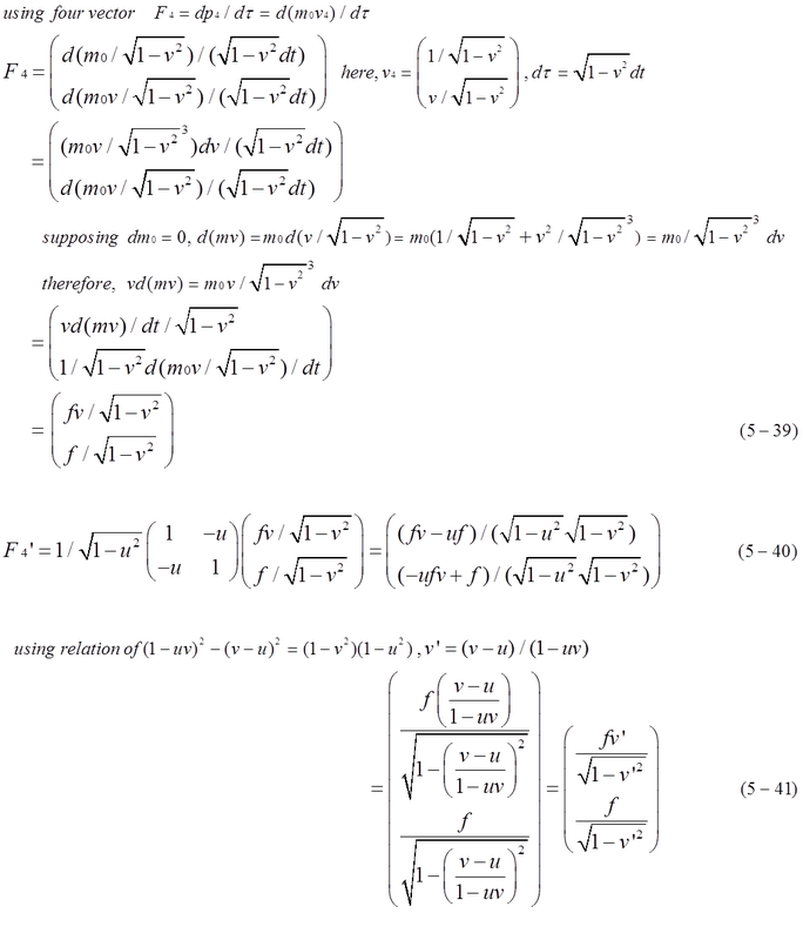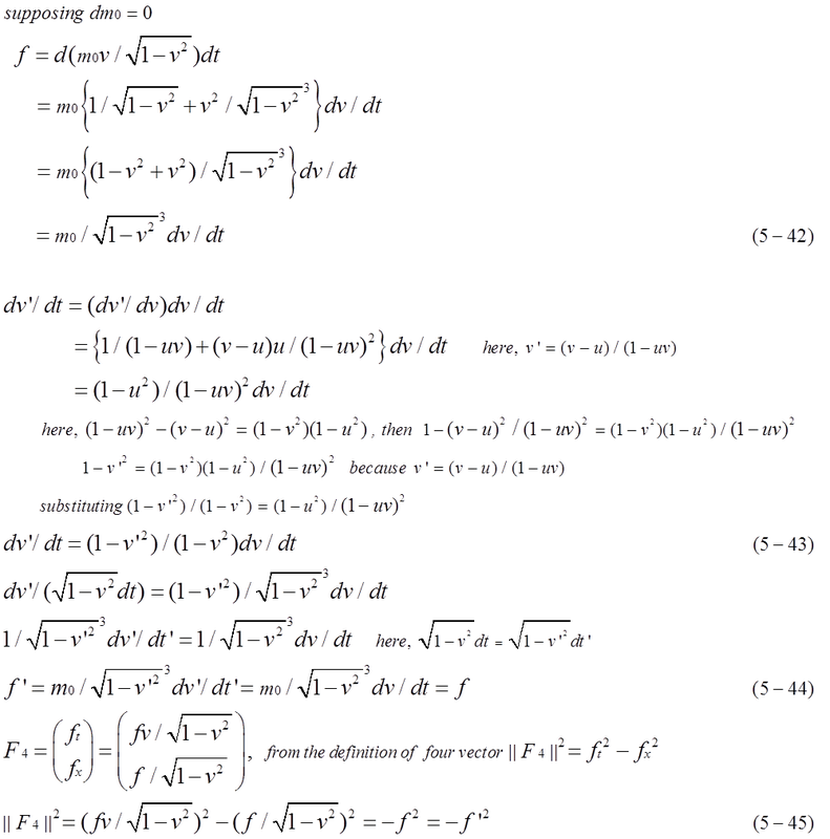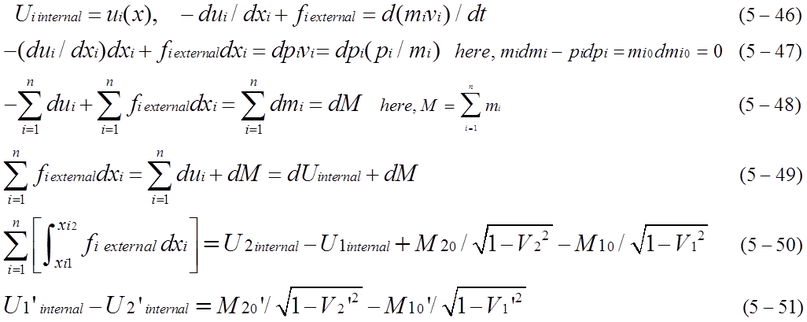4. Increase of energy in the system is equal to increase of mass in case of free particles. (dE=dM=FdX)
At first , explanation is limited to one dimension of t-x. By differentiating equation (2-17), equation (4-1),(4-2) are obtained if rest mass M0 neither increases nor decreases. In this case, the motion of M can be treated in the same way of a single mass.
At first , explanation is limited to one dimension of t-x. By differentiating equation (2-17), equation (4-1),(4-2) are obtained if rest mass M0 neither increases nor decreases. In this case, the motion of M can be treated in the same way of a single mass.
On condition that X is a representative position of mass M, increase of energy is expressed as following equation.
Substituting P/M=dM/dP, dE=dM is obtained as equation (4-3). Here, F is the external force.
Both in Newtonian and relativistic mechanics, F equals dP/dt=d(MV)/dt. In the case that M is always M0, F equals M0(dV/dt)
in Newtonian mechanics. There are many people who believe that F always equals M0(dV/dt) in Newtonian mechanics.
However, there are some exceptions. In Tsiolkovsky rocket equation, F equals dP/dt because the fuel of rocket is exhausted.
In equation (4-3), dM is merely increase of visible kinetic energy. There is no increase of rest mass. V=dX/dt can be defined as a representative velocity. We must remember each of resolved mass has complex motion in the micro world.
Substituting P/M=dM/dP, dE=dM is obtained as equation (4-3). Here, F is the external force.
Both in Newtonian and relativistic mechanics, F equals dP/dt=d(MV)/dt. In the case that M is always M0, F equals M0(dV/dt)
in Newtonian mechanics. There are many people who believe that F always equals M0(dV/dt) in Newtonian mechanics.
However, there are some exceptions. In Tsiolkovsky rocket equation, F equals dP/dt because the fuel of rocket is exhausted.
In equation (4-3), dM is merely increase of visible kinetic energy. There is no increase of rest mass. V=dX/dt can be defined as a representative velocity. We must remember each of resolved mass has complex motion in the micro world.
Equation (4-4),(4-5),(4-6) are satisfied in case of 3 dimensional space. Representative momentum P is proportional to representative velocity V. That is, Px=MVx, Py=MVy, Pz=MVz. dE is inner product of external force (Fx,Fy,Fz) and displacement (dX, dY,dZ).
As equation (4-6) is shown, dE=dM is introduced in case of 3 dimensional space.
In equation (4-1), (4-6), it is supposed that increase of dM0 is zero. However, we should know there are some cases that rest mass M0 is kept invariant even if M0 either increases or decreases. For example, a flying object which is receiving air resistance increases inner kinetic energy (thermal energy) although the increase of mass is negligible. The meaning of invariant is not constant but common in any inertial reference frame.
In equation (4-1), (4-6), it is supposed that increase of dM0 is zero. However, we should know there are some cases that rest mass M0 is kept invariant even if M0 either increases or decreases. For example, a flying object which is receiving air resistance increases inner kinetic energy (thermal energy) although the increase of mass is negligible. The meaning of invariant is not constant but common in any inertial reference frame.
5. Modification of F=dP/dt=d(MV)/dt in the theory of special relativity
Some people insist that special relativity can not be applied to accelerated motion. These people are confusing the motion of an object with the motion of coordinates. The accelerated motion can be described in any inertial coordinate. The equation of accelerated motion is expressed by four-vector. In general, influence on inner particles can be negligible. However, on rare occasion, the equation of motion should be given considering invariant M0(rest mass) is not constant.
In this chapter, visible kinetic energy of mass and inner kinetic energy are considered. To simplify the equation, the dimension of coordinates is limited to t-x.
An object is moving in coordinates A. Another inertial coordinates B is moving with velocity u in the coordinates A. Velocity u is uniform in coordinates A. (t,x) and (t',x') are transformed by Lorentz transformation shown in equation (5-1),(5-2),(5-3).
Some people insist that special relativity can not be applied to accelerated motion. These people are confusing the motion of an object with the motion of coordinates. The accelerated motion can be described in any inertial coordinate. The equation of accelerated motion is expressed by four-vector. In general, influence on inner particles can be negligible. However, on rare occasion, the equation of motion should be given considering invariant M0(rest mass) is not constant.
In this chapter, visible kinetic energy of mass and inner kinetic energy are considered. To simplify the equation, the dimension of coordinates is limited to t-x.
An object is moving in coordinates A. Another inertial coordinates B is moving with velocity u in the coordinates A. Velocity u is uniform in coordinates A. (t,x) and (t',x') are transformed by Lorentz transformation shown in equation (5-1),(5-2),(5-3).
Infinitesimal space dx and infinitesimal time dt are also expressed by equation (5-4), (5-5). It is necessary to use dx and dt for accelerated motion as Newtonian mechanics used dx and dt. Supposing that an object is moving with velocity V in coordinates A, the equation of motion is given. If the object is observed in coordinates B, the velocity of the object is V' in coordinates B. To express the motion of the object, infinitesimal displacement dx=Vdt and dx'=V'dt' are introduced. Substituting equation (5-6) into equation (5-4), (5-5), equation (5-7) is obtained. We must not confuse V, V' and u (velocity of coordinates B). While the motion of the object is not necessarily uniform, coordinates A and B are inertial system.
Equation (5-7) is exactly the formula of velocity composition. Therefore, V and V' are expressed by equation (5-8). Even if V' and u are close to 1, V approaches 1 and never exceeds 1 (light speed).
It is necessary to review the concept of invariant s. s and ds are invariant in any reference frame. s and ds are equal to s' and ds' respectively. Not to mention, s and s' are not always constant. s^2 and ds^2 are expressed by equation (5-9),(5-10),(5-11).
s and ds are invariant because (t,x) is inertial coordinates regardless of accelerated motion of the object. We must distinguish (ds)^2 and d(s^2). Substituting equation (5-6), (5-8) into equation (5-11), similar two equation (5-12), (5-13) are obtained. ds^2=ds'^2 is guaranteed because coordinates A is transformed to coordinates B by Lorentz matrix.
s and ds are invariant because (t,x) is inertial coordinates regardless of accelerated motion of the object. We must distinguish (ds)^2 and d(s^2). Substituting equation (5-6), (5-8) into equation (5-11), similar two equation (5-12), (5-13) are obtained. ds^2=ds'^2 is guaranteed because coordinates A is transformed to coordinates B by Lorentz matrix.
Substituting equation (5-6) into equation (5-5), equation (5-14) is obtained. Equation (5-14) indicates the relation between dt and dt'. By substituting equation (5-14) to equation (5-13), equation (5-15) is obtained. Then, ds=sqrt(1-V^2)dt=sqrt(1-V'^2). Especially, when displacement of motion is dx=vdt, infinitesimal proper time can be defined as equation (5-16). Infinitesimal proper time is also invariant in the coordinates A and B, and it represents the time elapsed in the instantaneous inertial coordinates whose velocity coincides with the velocity of the object for an infinitesimal time. We must notice that the velocity of the object is equal to zero in the instantaneous coordinates. Then, infinitesimal time becomes proper time. Although it is redundant, someone may doubt that equation (5-14) and (5-16) are consistent. dt'/dt=(1-Vu)/sqrt(1-u^2)=sqrt(1-v^2)/sqrt(1-v'^2) is confirmed by substituting equation (5-8) into equation (5-16).
Preparation for modification of F=dp/dt is completed. Although dE=dM is already shown in equation (4-3), dE=dM is proved in different way. In the first case, rest mass M0 is supposed to be constant value. This means that external force does not affect inner rest mass and inner kinetic energy. Equation of motion is expressed as equation (5-17) again. Two terms are colored in equation (5-18). Blue term is related to rest mass and red term is related to kinetic energy. In the first case, dM0 is zero. dM is equal to dE from equation (5-18),(5-19). However, there is no increase of rest energy because dM0 is supposed to be zero.
In the second case, rest mass M0 is not supposed to be constant value. External force affects inner rest mass and inner kinetic energy. F=dP/dt is the same as equation (5-17), (5-20). dM is expressed by equation (5-21). F(external force) has two colored terms. The first term is related to M0. The second term is related to kinetic energy. Some parts of M0 is independently accelerated by the component of external force. Equation (5-23) is obtained dividing both side of equation (5-22) by sqrt(1-V^2). Equation of motion is described by four-vector as equation (5-23), (5-24). Considering dM0, the change of momentum is not M0dV4 but d(M0V4).
When dM0 is not zero, inner kinetic energy either increases or decreases by external force. Each composition of rest mass should be considered. dE is not equal to FdX. dE is equal to f1dx1+f2dx2+------+fnxn because dX is not equal to dx1,dx2,----dxn. Representative position X expressed by equation (5-27) is not clear. On the other hand, (M ,P) and V=P/M are clearly defined in equation (2-11), (3-5), (3-6), (3-7), (3-8).
As shown in equation (5-26), (5-28), FdX is not equal to dM while dE is equal to summation of fidxi. Calculation of FdX is wrong. However, it is expected dM is equal to dE from conservation of energy.
When the motion of inner rest mass is considered, it is difficult to calculate all the motion of infinitesimal mass. Equations from (5-29) to (5-32) is the result of calculation of the decomposed rest mass mi. Partial increase of dE is equal to dmi when dmi0 is zero. dmi0=0 does not mean dM0=0 because inner momentum pi increases or decreases.
As shown in equation (5-29), there are internal forces which are caused during the collision between mi and mj. There might be other internal forces as inner potential force.
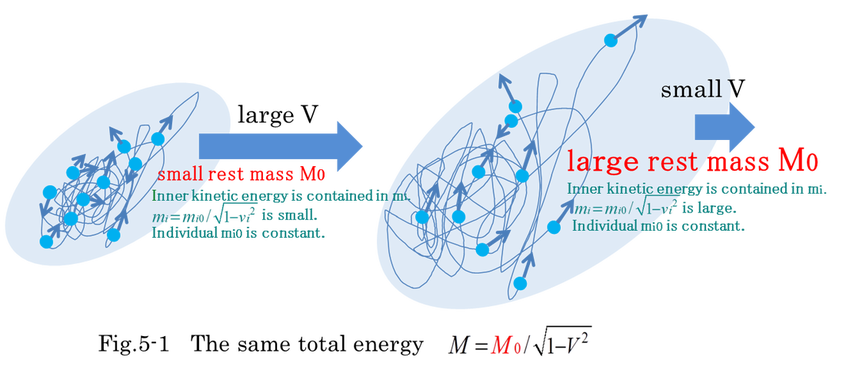
Equation (5-35) indicates summation of fi internal*dxi=0 because reaction force cancels each other. When internal structure like elastic element does not exist, summation of fi internal*dxi=0. Then, increase of fi external*dxi turns into visible kinetic energy and inner kinetic energy. Finally, dE is equal to dM under the condition of dmi0=0. Even if dE increases, it depends on MV (macro momentum P) whether M0 increases or decreases. From the equation of M0^2=M^2-P^2, it is possible that inner kinetic energy of M0 decreases. When inner kinetic energy decreases and visible kinetic energy increases at the same time by external force, M0 decreases. Fig.5-1 indicates the case that relativistic mass is the same even if rest mass M0 has different inner kinetic energy. From Fig.5-1, it is possible to image that rest mass M0 is partly made of inner kinetic energy. As a matter of course, M0 also contains a lot of mi0.
Integration of dE is equation(5-36) when vi changes from vi1 to vi2. Even if M0 changes, rest mass M0 can be defined as equation (5-37), (5-38). In this case, M and M0 change though M0 is invariant. Moving mass M1 and M2 can be transformed to M10 and M20 respectively in the instantaneous coordinate whose velocity u must be varied from V1 to V2. V1 and V2 are the velocity of object observed from inertial coordinate A. As far as the coordinates A is inertial frame, the equation of accelerated motion is described as equation (5-23), (5-32). When rest mass is affected by external forces, rest mass of a group of mass changes from M10 to M20.
Following equations indicate four-vector of force F4. According to formula of F4, F4 is equal to ( f*v/sqrt(1-v^2), f/sqrt(1-v^2) ). The first component is the rate of change in energy. The second component is the rate of change in momentum. As shown in equation (5-40), force F4 in coordinates A can be transformed to F4' in coordinates B which is moving with velocity u in coordinates A. Equation (5-41) shows that force F4 has the same style in different coordinates B. However, f=f ' must be proved in order to consider F4 to be four-vector.
Equation (2-3), (2-6) are useful. Equation (5-42), (5-43), (5-44) indicate f=f'. In considering four-vector of force, the relation between f and f ' is expressed by equation (5-45) in t-x dimension.
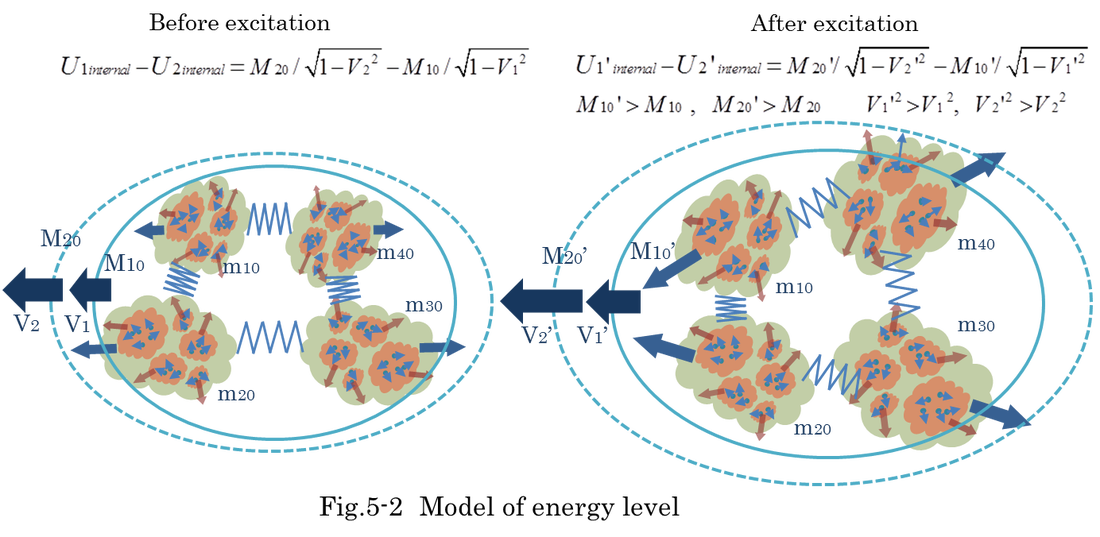
Internal potential energy Uinternal is supposed to be dependent on position of x. Including external energy and Internal potential energy, the relation between Uinternal, external energy and mass satisfies equation (5-46), (5-47), (5-48), (5-49). Integration of energy is equation (5-50). When external energy is zero, total of Uinternal and M is constant. That is dU=-dM. As it is explained in chapter 2, M includes visible kinetic energy and rest energy. As shown in equation (5-50), when the effect of external energy is large enough to change the internal potential energy, the change of internal potential energy causes the change of visible kinetic energy and rest energy(rest mass). Of course, there is a case M10=M20. After the excitation by external forces, different energy level remains stable as shown in equation (5-51). Fig.5-2 shows the model of energy level. When internal potential energy exists in the system, the increase of total energy is not equal to dM. That is, dE=fexternal*dx= dM+dU.( refer to Fig ap10-9 in appendix-10.)